Silencejql
0%

AlgorithmLearning-汉诺塔(分治递归)

发表于 分类于 ， Valine：
本文字数： 1.8k 阅读时长 ≈ 2 分钟

利用分治处理汉诺塔问题

问题

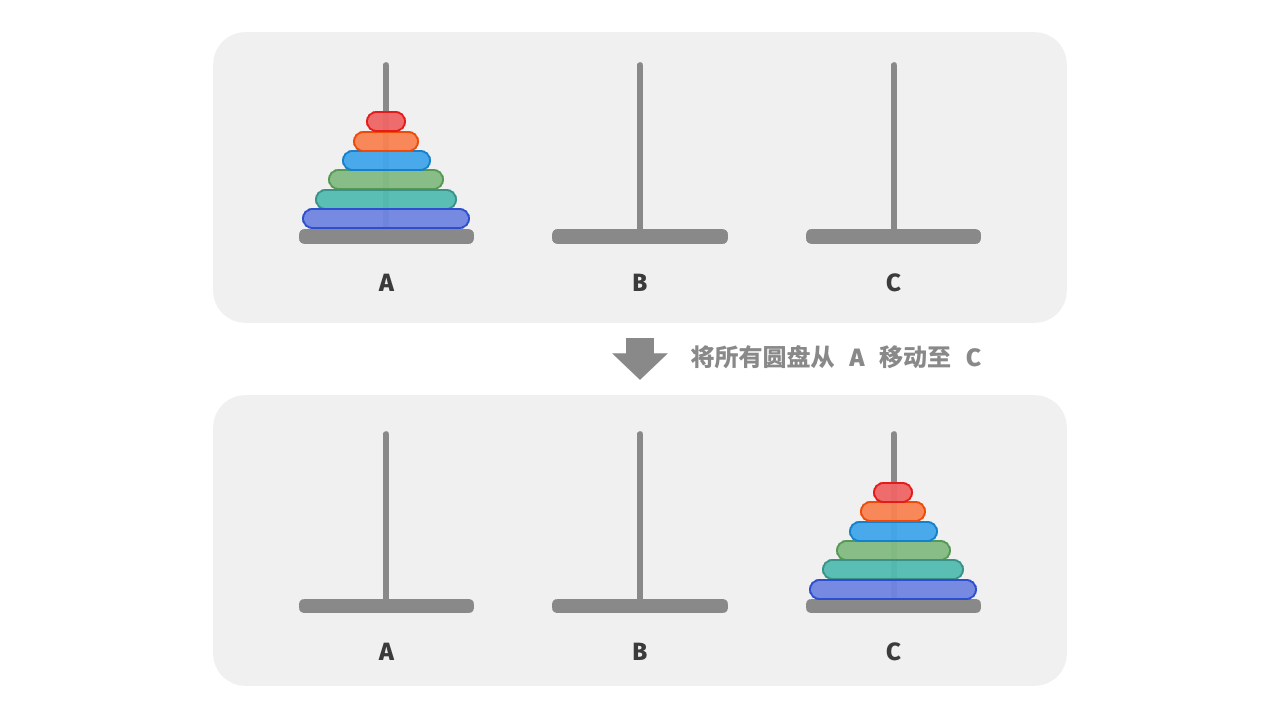
给定三根柱子，记为 A、B 和 C 。起始状态下，柱子A 上套着 𝑛 个圆盘，它们从上到下按照从小到大的顺序排列。我们的任务是要把这 𝑛 个圆盘移到柱子C 上，并保持它们的原有顺序不变

  1. 圆盘只能从一根柱子顶部拿出，从另一根柱子顶部放入。
  2. 每次只能移动一个圆盘。
  3. 小圆盘必须时刻位于大圆盘之上。
    ![[Pasted image 20250619133250.png]]

问题分析

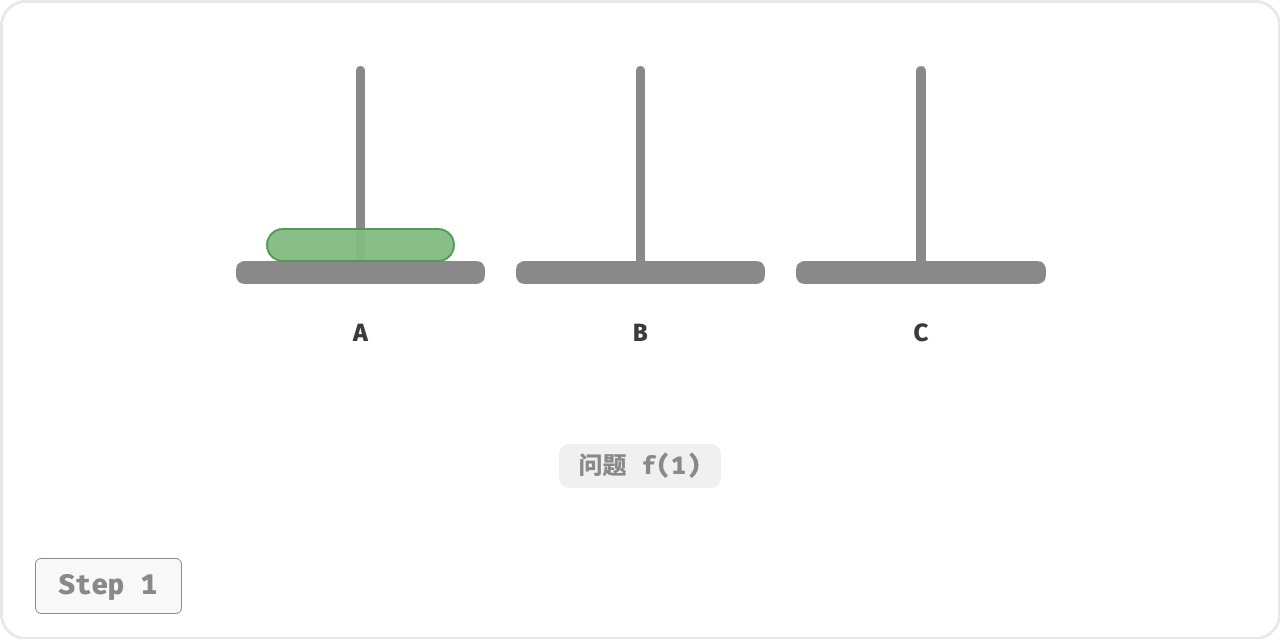
对于问题 𝑓(1)

即当只有一个圆盘时，我们将它直接从 A 移动至 C 即可
![[Pasted image 20250619133711.png]]

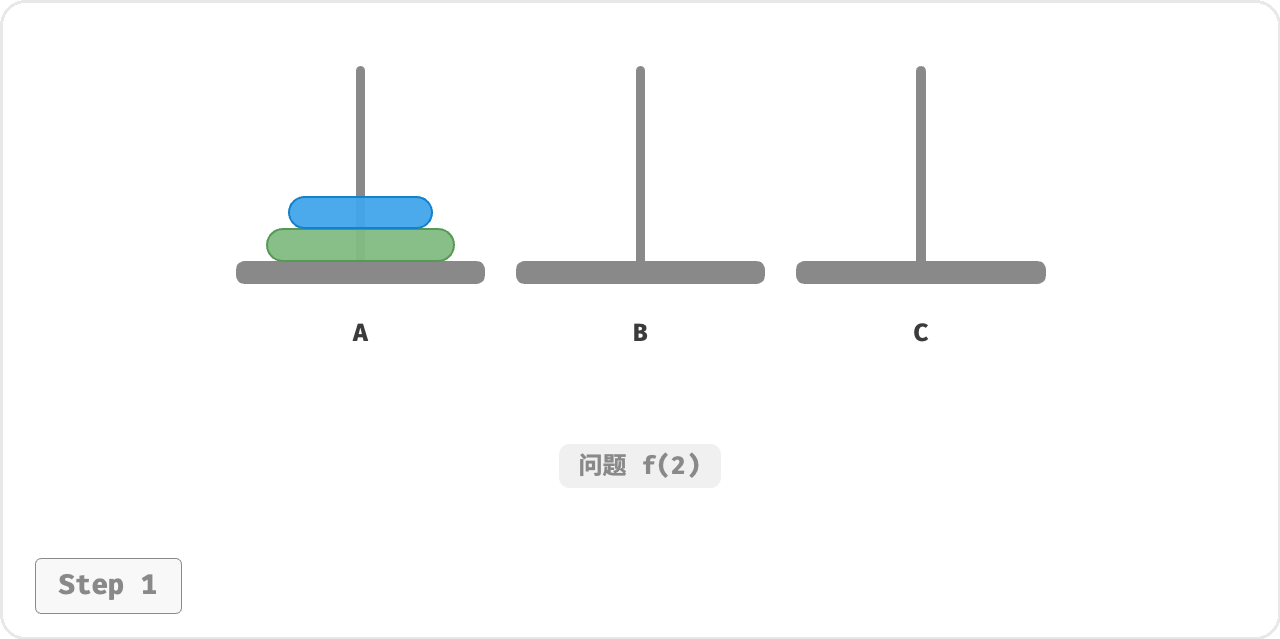
对于问题 𝑓(2)

即当有两个圆盘时， 由于要时刻满足小圆盘在大圆盘之上，因此需要借助
B 来完成移动。

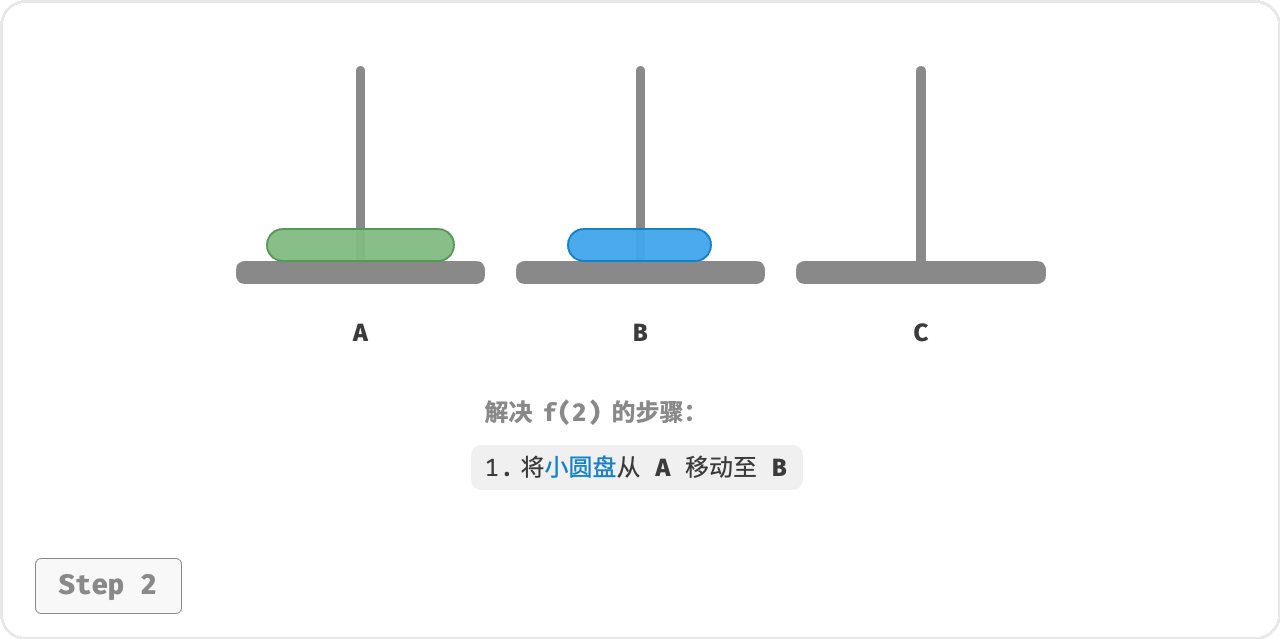
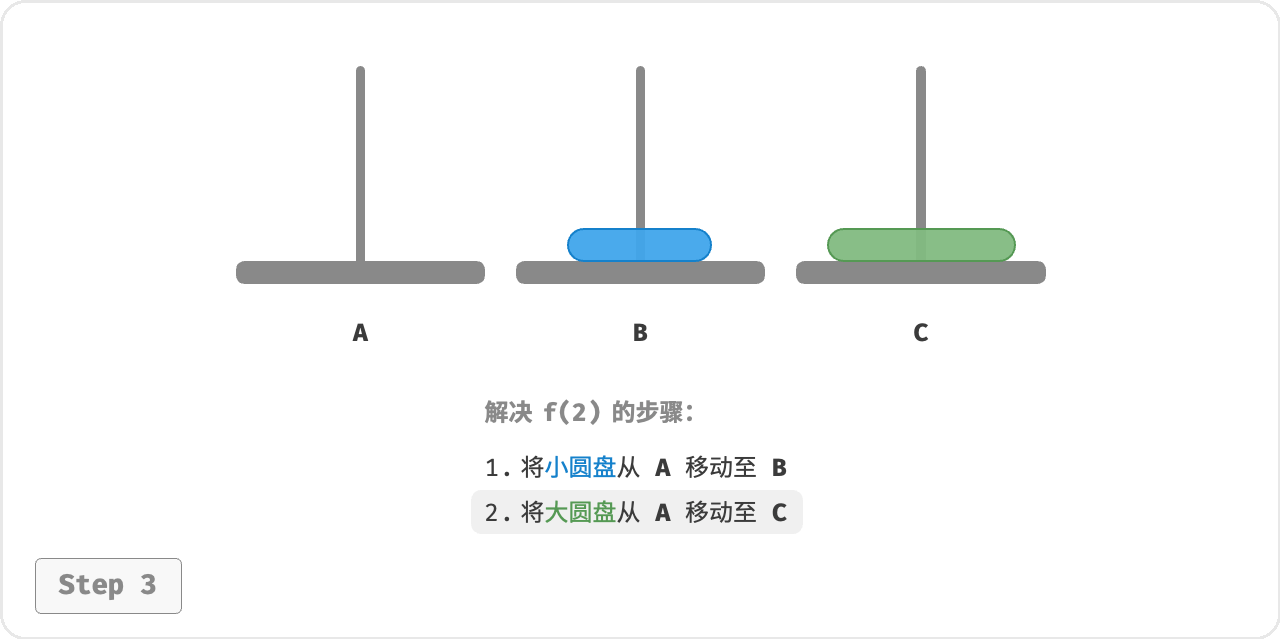
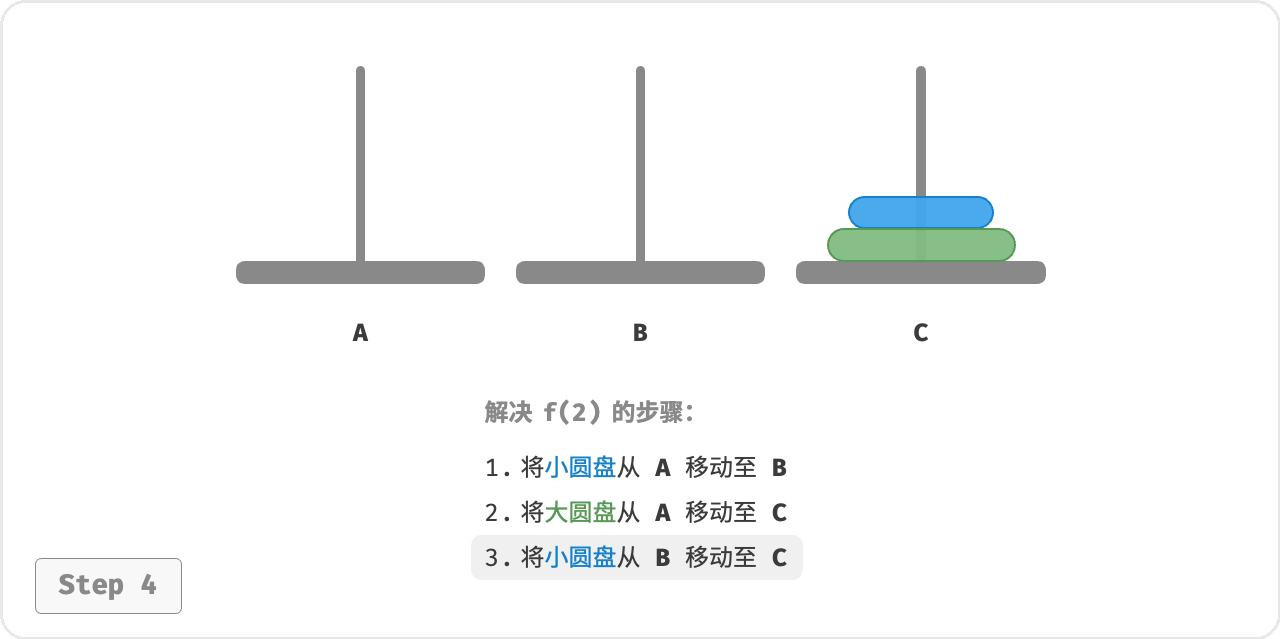
  1. 先将上面的小圆盘从 A 移至 B 。
  2. 再将大圆盘从 A 移至 C 。
  3. 最后将小圆盘从 B 移至 C 。
    解决问题 𝑓(2) 的过程可总结为： 将两个圆盘借助 B 从 A 移至 C 。其中，C 称为目标柱、B 称为缓冲柱。
    ![[Pasted image 20250619133805.png]]
    ![[Pasted image 20250619133825.png]]
    ![[Pasted image 20250619133831.png]]
    ![[Pasted image 20250619133835.png]]

对于问题 𝑓(3)

即当有三个圆盘时，情况变得稍微复杂了一些。
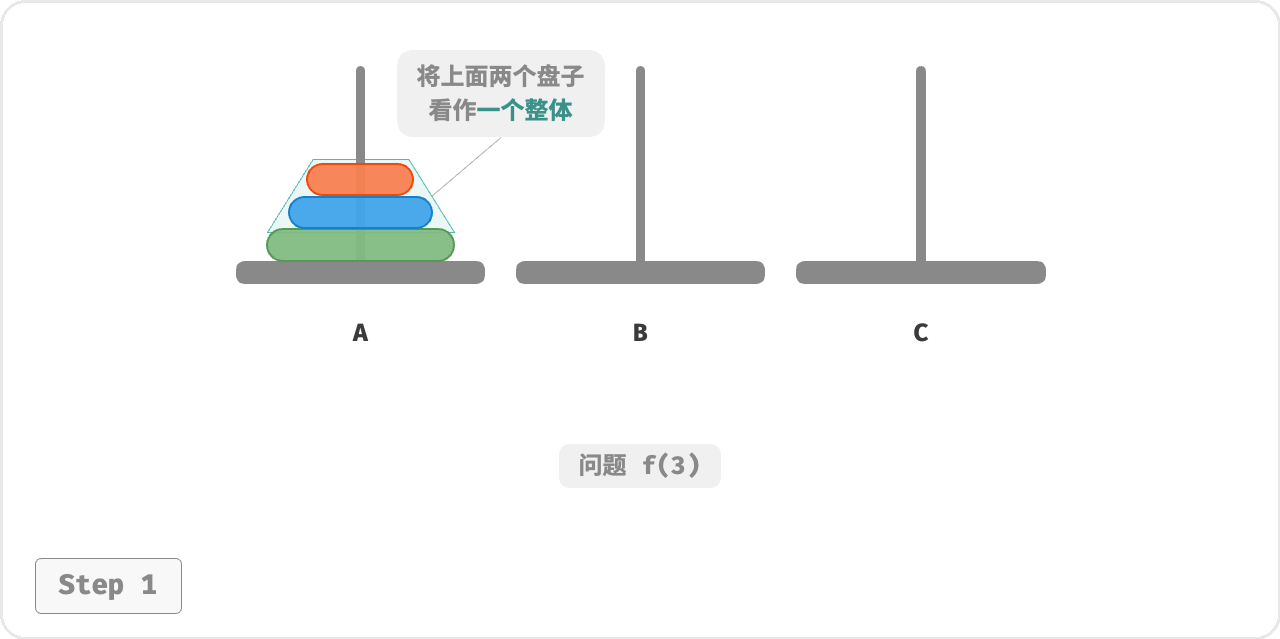
因为已知 𝑓(1) 和 𝑓(2) 的解，所以我们可从分治角度思考， 将 A 顶部的两个圆盘看作一个整体, 这样三个圆盘就被顺利地从 A 移至 C 了。

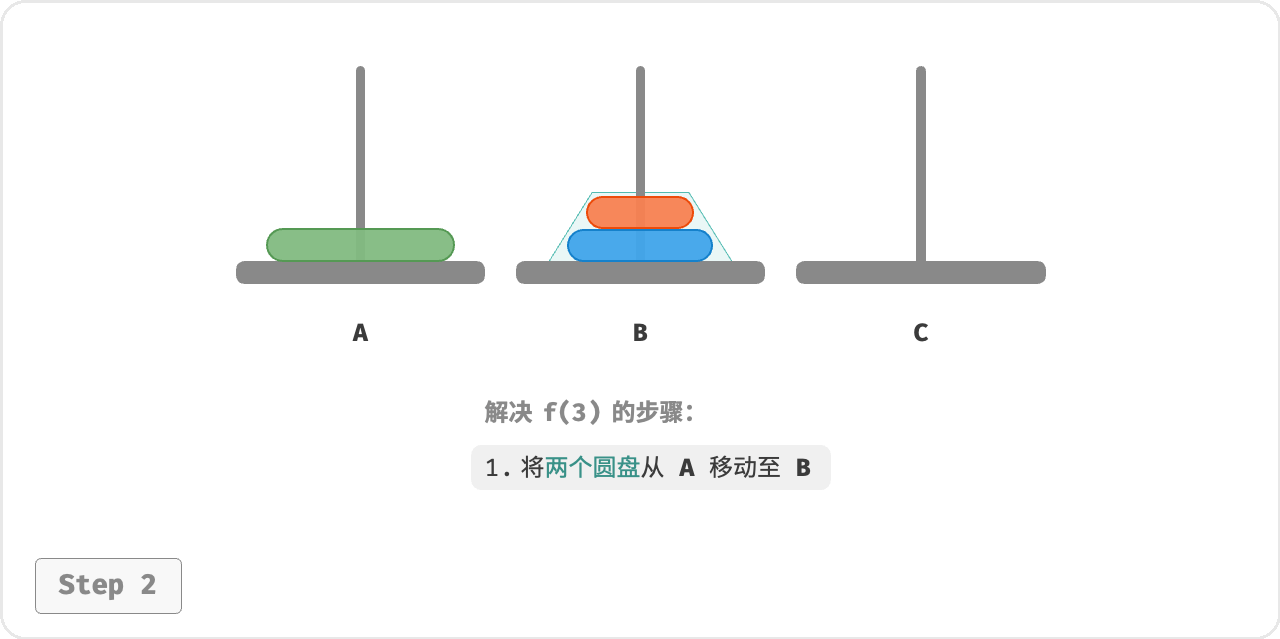
  1. 令 B 为目标柱、 C 为缓冲柱，将两个圆盘从 A 移至 B 。
  2. 将 A 中剩余的一个圆盘从 A 直接移动至 C 。
  3. 令 C 为目标柱、 A 为缓冲柱，将两个圆盘从 B 移至 C 。
    ![[Pasted image 20250619133859.png]]
    ![[Pasted image 20250619133903.png]]
    ![[Pasted image 20250619133907.png]]
    ![[Pasted image 20250619133919.png]]

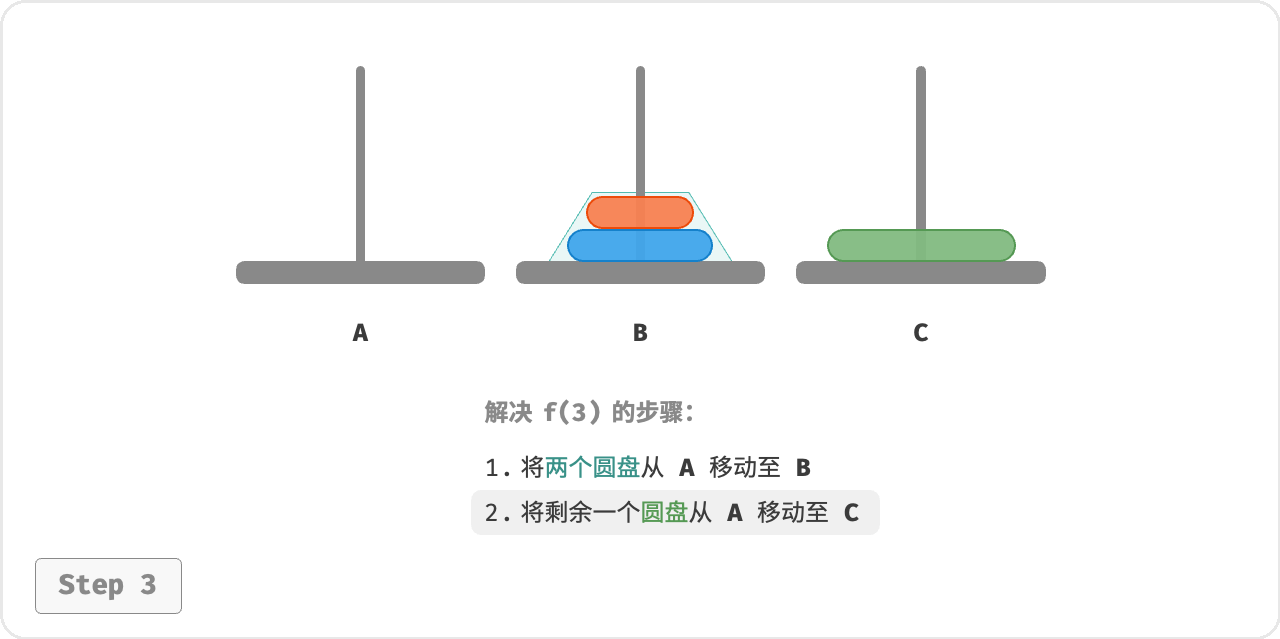
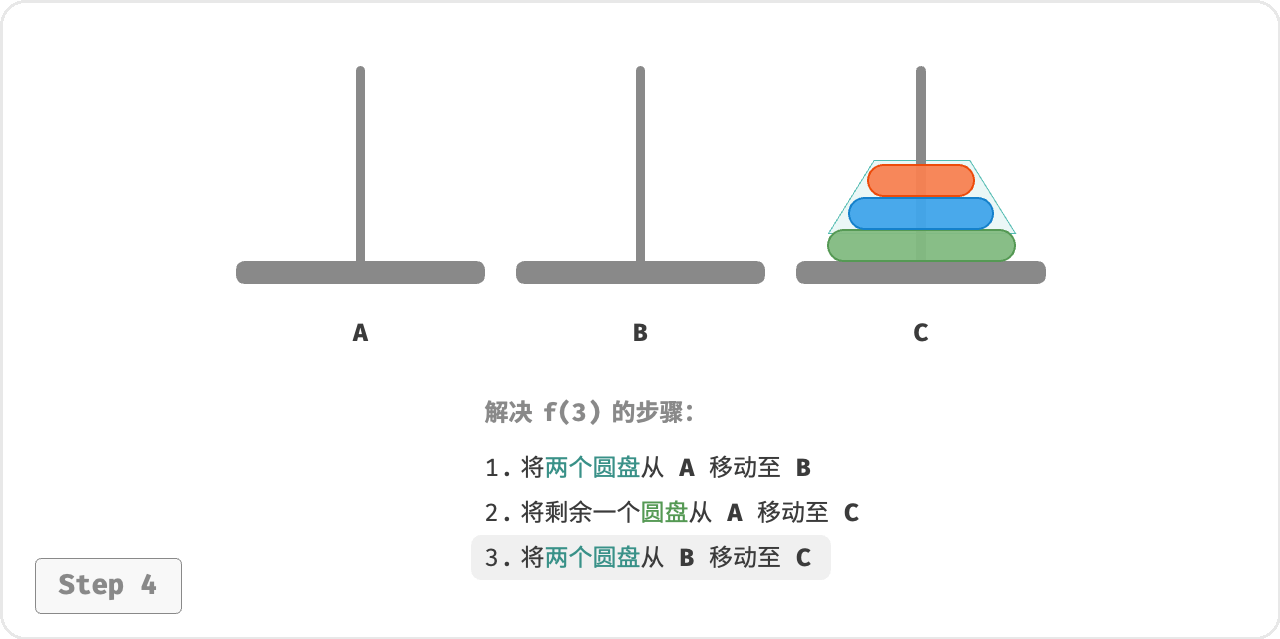
从本质上看， 我们将问题 𝑓(3) 划分为两个子问题 𝑓(2) 和一个子问题 𝑓(1) 。按顺序解决这三个子问题之后，
原问题随之得到解决。这说明子问题是独立的，而且解可以合并。
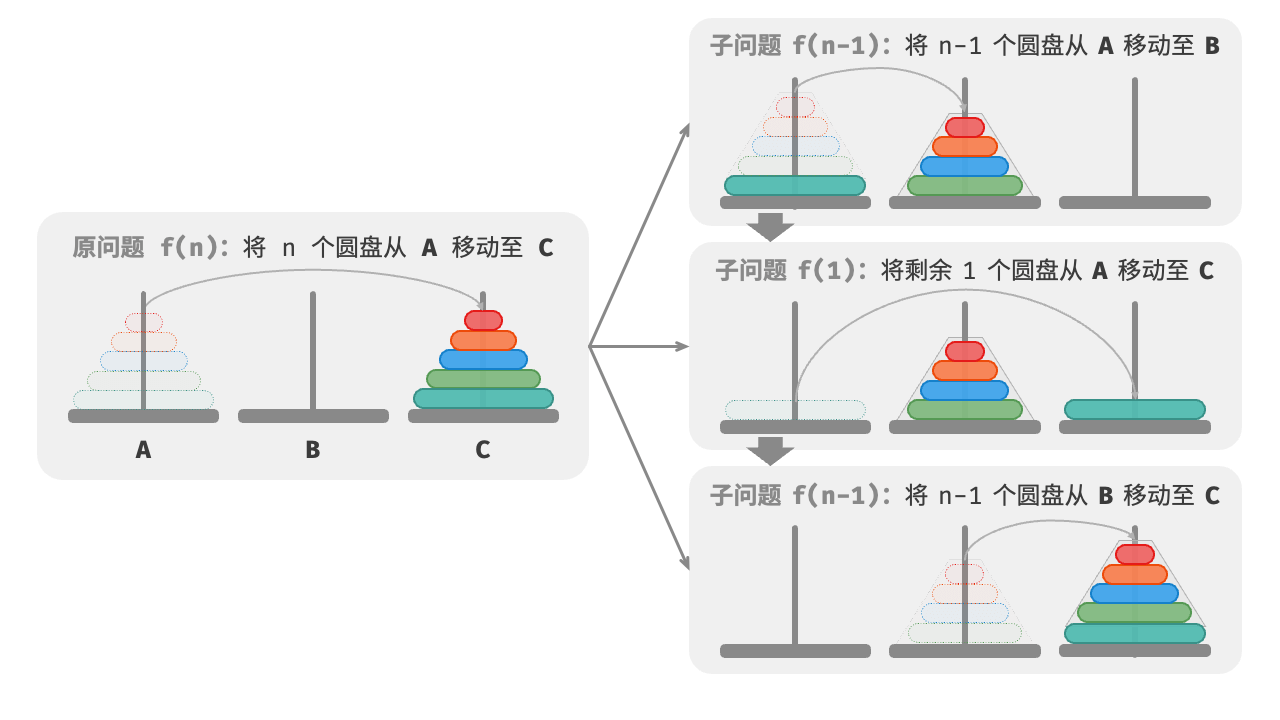
至此，我们可总结出下图所示的解决汉诺塔问题的分治策略：将原问题 𝑓(𝑛) 划分为两个子问题 𝑓(𝑛-1)
和一个子问题 𝑓(1) ，并按照以下顺序解决这三个子问题。

  1. 将 𝑛 - 1 个圆盘借助 C 从 A 移至 B 。
  2. 将剩余 1 个圆盘从 A 直接移至 C 。
  3. 将 𝑛 - 1 个圆盘借助 A 从 B 移至 C 。
    对于这两个子问题 𝑓(𝑛 - 1) ， 可以通过相同的方式进行递归划分，直至达到最小子问题 𝑓(1) 。而 𝑓(1) 的
    解是已知的，只需一次移动操作即可。
    ![[Pasted image 20250619133615.png]]

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/* 移动一个圆盘 */  
void Move(List<int> src, List<int> target) {  
	// 从 src 顶部拿出一个圆盘  
	int pan = src[^1];  
	src.RemoveAt(src.Count - 1);  
	// 将圆盘放入 target 顶部  
	target.Add(pan);  
}
/* 求解汉诺塔问题 f(i) */  
void DFS(int i, List<int> src, List<int> buffer, List<int> target) {  
	// 若 src 只剩下一个圆盘，则直接将其移到 target  
	if (i == 1) {  
		Move(src, target);  
		return;  
	}  
	// 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 target 移到 buffer  
	DFS(i - 1, src, target, buffer);  
	// 子问题 f(1) ：将 src 剩余一个圆盘移到 target  
	Move(src, target);  
	// 子问题 f(i-1) ：将 buffer 顶部 i-1 个圆盘借助 src 移到 target
	DFS(i - 1, buffer, src, target);  
}
/* 求解汉诺塔问题 */  
void SolveHanota(List<int> A, List<int> B, List<int> C) {  
	int n = A.Count;  
	// 将 A 顶部 n 个圆盘借助 B 移到 C  
	DFS(n, A, B, C);
}